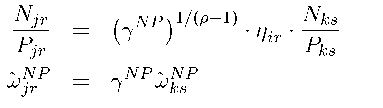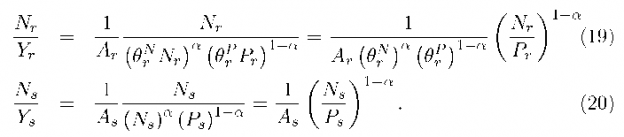A FPEQ and generalized cost functions In this appendix, we consider tests of FPEQ for alternate cost functions using the factor share methodology developed for the CES production function. A1. The translog cost function The translog cost function with constant returns to scale is given by Subject to the usual restrictions to ensure homogeneity in prices, the factor shares, sj = wjxj/c(wj, Y), are linear in the parameters and are given by Under the null…
Tag: FACTOR PRICE EQUALITY
In this paper, we provide a general methodology to test for factor price equality across economies. Under the usual HO assumptions of common products, common product prices, and common technologies, we develop testable implications of the Factor Price Equality Theorem and the Relative Factor Price Equality Theorem for a broad class of production technologies. Unlike previous attempts to formulate tests for FPEQ and RFPEQ, our testing methodology is robust to sources of unobserved heterogeneity that…
As described above, an additional implication of multiple factor price cones is that regions in non-neighboring cones are expected to have distinct mixes of goods. By determining the relationship between product mix overlap and cone assignments for pairs of regions, we can provide a robustness check on our results. More specifically, we estimate the number of industries two regions have in common as a function of their cone assignments where Irs is the number of…
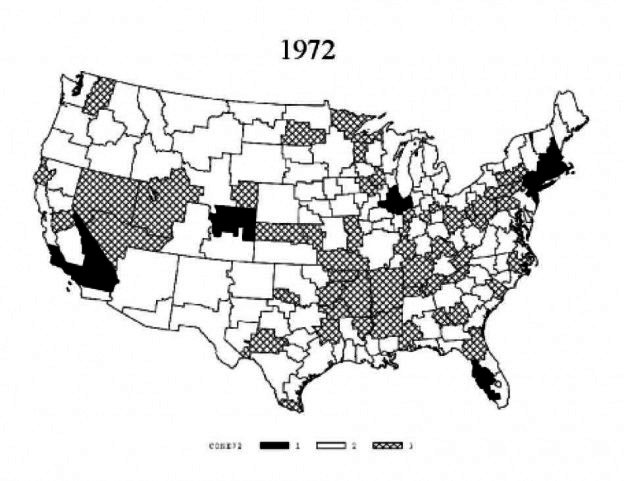
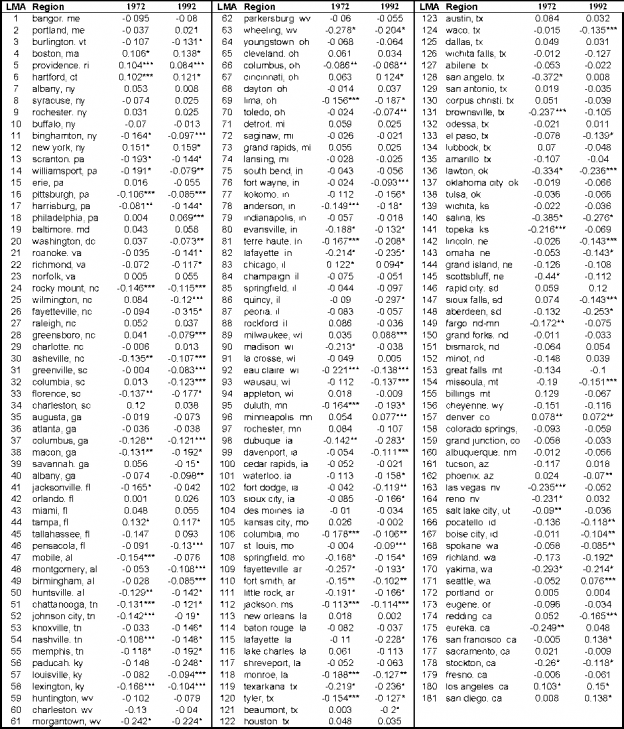
From Figure 9, we know that the single cone hypothesis can be easily rejected. Using those results and the methodology described above, we can produce factor price cones within the US based on relative wages for 1972 and 1992. Regions with significantly higher wagebill ratios are grouped in cone 1. For 1972, there are eight regions in this upper cone including large, urban labor markets such as New York City, Chicago, and Los Angeles. Regions…
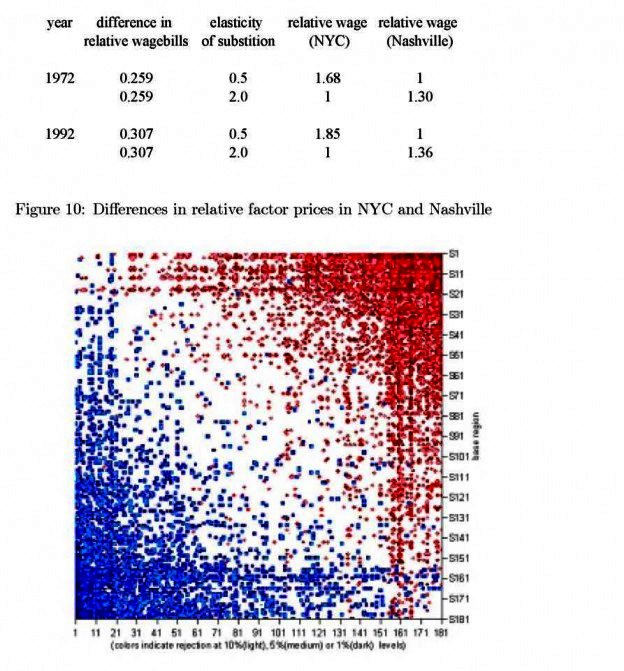
We can now answer the question posed at the outset. Nashville and New York have significantly different relative wagebills for non-production and production workers, and thus significantly different relative wages. In fact, in 1972 the relative wagebill in Nashville is 11 percent below the US average while that for New York is 15% above. To map the estimated coefficients into differences in relative factor prices, we need to make assumptions about the elasticity of substitution….
As is well known, the LRD only collects wage information on two categories of workers, production and non-production. However, we avoid the usual criticism that dividing workers into production and non-production groups imperfectly classifies them according to skill as our methodology is robust to unobserved differences in regional factor quality. More important for our purposes is that any imperfections in the allocation of workers to production and non-production categories be similar across regions within an…
In this section we consider econometric issues that may cause us to mistakenly reject RFPEQ. Product misclassification can cause us to reject RFPEQ spuriously. To see why, suppose that industry i comprises two goods, j and k, and that good j is non-production worker intense relative to good k by a factor of n*r (e.g. stylish dress shirts versus ordinary dress shirts).15 In addition, to keep things simple, assume there are no factor quality differences…
Second, we test RFPEQ by estimating equations 13 and 14 for all industry and region-pair combinations. We start by choosing a region to be the benchmark, i.e. 7B = 1. Then we run a regression of the form: or where the dr ’s are region dummies that equal one whenever region r is the independent variable. Testing whether the afB’s are jointly equal to zero provides a test of the null hypothesis of a single…
Solving for the input-output ratios in terms of the ratio of observed factor inputs in the two regions, we get Rearranging terms, we can write the observed factor inputs in terms of the observed unit factor requirements, Under the maintained hypothesis of RFPEQ, we can solve for the relationship between the observed factor ratios by equating the relative wages paid to the true labor inputs across the regions, yielding In words, the observed, unadjusted, input…
The previous section has detailed testable implications of relative factor price equality across regions. It is still possible for absolute factor price equality to fail even if RFPEQ holds. Factor-independent productivity shifters will leave relative factor prices unaltered but change the levels of the factor rewards for all factors. In this section we consider the testable implications of FPEQ. The relationship between rewards for a given factor across regions is given by Again the regional…