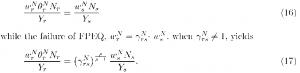The previous section has detailed testable implications of relative factor price equality across regions. It is still possible for absolute factor price equality to fail even if RFPEQ holds. Factor-independent productivity shifters will leave relative factor prices unaltered but change the levels of the factor rewards for all factors. In this section we consider the testable implications of FPEQ.
The relationship between rewards for a given factor across regions is given by
Again the regional differences in factor quality, 0^, are unobserved so we cannot use the unit factor inputs to test for FPEQ. We can, however, employ the factor shares, under FPEQ
Of course, this relationship holds for all the factors in the production function. To reject FPEQ, we need only reject (7^) = 1 for one single factor.10 In the next section, we outline our strategy for estimation with its advantages and disadvantages relative to existing methodologies.
4. Econometric Methodology
In this section, we start by discussing possible problems that have arisen in the existing empirical literature on testing FPEQ and RFPEQ. We then outline an empirical methodology for testing the null hypothesis of one RFPEQ cone versus the alternative of multiple RFPEQ cones. In the event that the null of one cone is not rejected, we describe a related method for testing for one FPEQ cone versus the alternative of multiple FPEQ cones. In the event that the single RFPEQ cone hypothesis is rejected, we present a technique for grouping regions into cones. Finally we conclude with an assessment of the pros and cons of our empirical methodology.
4.1. Unit input requirements
Observed unit factor requirements have been used in several recent papers on testing predictions of the HO model, e.g. Hanson and Slaughter (1999) and Davis and Weinstein (1998). We argue in this section that unit factor requirements cannot be used to determine whether two regions have common relative factor prices unless there are (1) no regional productivity differences and (2) no differences in regional factor quality. We simplify the discussion by focusing on the special case of a Cobb-Douglas production function with two (labor) inputs (N and P), constant returns to scale, variations in regional labor quality, and regional productivity differences. The production functions for the industry in the two regions are given by
Each region has a Hicks-neutral productivity shifter, A., and the two types of labor in region r differ in quality (productivity) from those in the benchmark region, s, by multiplicative factors, Of and Of. These productivity shifters do not vary across industries within a region. Only industry value-added, Yi and unadjusted labor inputs, Ni and Pi can be observed.