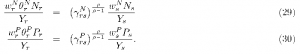Second, we test RFPEQ by estimating equations 13 and 14 for all industry and region-pair combinations. We start by choosing a region to be the benchmark, i.e. 7B = 1. Then we run a regression of the form:
or
where the dr ’s are region dummies that equal one whenever region r is the independent variable. Testing whether the afB’s are jointly equal to zero provides a test of the null hypothesis of a single cone versus the alternative of multiple cones. Rejecting afB = 0 is sufficient to reject the hypothesis of RFPEQ between regions. Any pair of regions are in the same RFPEQ cone ii aJrB =aJsB.
When testing the null of one RFPEQ cone versus the alternative of multiple cones, we can reject the null if any region is significantly different from the benchmark region for a single factor pair. However, equation 27 cannot be run if the benchmark region has no (or few) industries in common with region r. As discussed above, this fact of no common industries by itself is not sufficient for us to categorize the regions as being in different cones. To avoid this problem in practice, and as a general robustness check, we run separate regressions allowing each region to be the benchmark region.
If we cannot reject the one cone hypothesis for relative factor prices, it still may be the case that absolute factor prices differ. In order to test the single cone hypothesis for FPEQ, we make use of equation 17 and test Yrs = 1 for each of the following two relationships
To reject FPEQ, we need only reject (7f)p p =1 for one single factor.13 The general form of the tests outlined above for RFPEQ works equally well in testing FPEQ, with the obvious substitution of the factor share in total costs in place of the relative wagebills. As before, the caveats about choosing benchmark regions apply.
4.4. Grouping regions into cones
If we reject the hypothesis that there is a single factor price cone, we must consider how to allocate regions to cones, i.e. which regions do face the same relative factor prices. We start with our specification using the entire US as the benchmark for an industry.
Our grouping procedure for a factor pair in a year is as follows:
1. Regress region-industry relative wagebills on that for the US (equation 26).
2. Any region that has a significantly higher wagebill ratio, i.e. a> 0, is placed in a High group while regions with significantly lower wagebill ratios, i.e. a< 0, are placed in a Low group. All remaining regions are placed in the Middle group. The only decision variable is the appropriate p-value.
3. Run equation 26 separately for each group of regions using only the regions in the cone to construct the benchmark wagebill ratio.
4. If no regions have coefficients significantly different from zero, then stop and use the three groups as cones.
5. If a region rejects, it is moved to a higher or lower group and repeat steps 3 and 4 until no regions switch groups.
This method has the advantage that the number of groups is chosen endogenously and all industries are used in allocating regions to groups. It has the disadvantage that two regions may end up in the same group even though their wagebill ratios are significantly different from one another. Alternative grouping procedures could use the pairwise regression coefficients from equation 28. Using these coefficients presents the problem that for 3 regions, A, B, and C, regions A and C may be significantly different from each other but neither may be significantly different from region B.