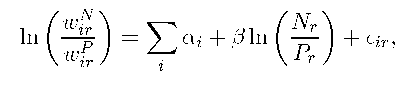Tag: FACTOR PRICE EQUALITY - Part 2

Now allow RFPEQ to fail so that the relative wage of quality adjusted non-production workers is 50% higher in region r (y _ 1.5) and to simplify the argument let a non-production worker in region r be equal to one third of a non-production worker in region s. From equation 11, we can see that observed relative non-production wages will be 50% lower in region r even though it is a region with high true…

Conversely, equation 10 implies that region r uses relatively fewer non-production workers than region s. These ratios might incorrectly lead one to assume that RFPEQ fails across these two regions and that region r has higher true relative wages. Without extra information on relative factor quality, neither observed wages nor observed factor quantities can help us disentangle the problem of RFPEQ versus differing input quality. To tackle this problem, we use data on both wages…

We start by developing the testable implications for relative factor price equality. Absent any ability to correctly adjust for factor quality differences, the observed relative labor wages in the two regions will be given by Under RFPEQ, the observed relative wages will only equal the true relative wages if the quality adjustments are the same for the two labor types across regions. For observed demands of the two labor types by the industry in the…

While we will make use of the theorems in looking for deviations from factor price equality (FPEQ) and relative factor price equality (RFPEQ) across regions within the US, the theory and empirical methodology can be applied to any tests of factor price equality. To develop our empirical framework, we impose some additional structure in the form of restrictions on the class of production functions. We restrict our analysis to the class of CES production technologies.7…

We now turn to a more formal examination of factor price equality across economic regions.6 We introduce the theorems that motivate our empirical framework and develop the testable implications of the theory under a relatively general set of assumptions. We start by restating the Factor Price Equality theorem of Leamer (1995) which provides the basis for our null and alternative hypotheses: Proposition 1 The Factor Price Equality Theorem (FPEQ). Regions producing the same mix of…

If we relax the standard assumptions of the Heckscher-Ohlin model it becomes much more difficult to distinguish empirically a multiple from a single cone equilibrium. Indeed, as indicated in figure 6, we are left with three types of tests: 1. PRODUCT MIX: If all regions produce the same group of sectors, the US is characterized by a single cone equilibrium.4 This implication is easy to verify but not very satisfying because the absence of production…

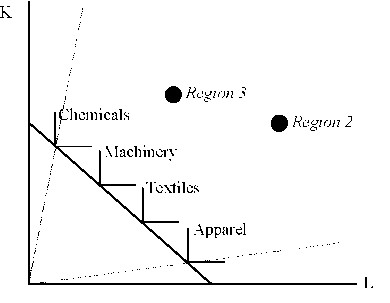
In the figure, the production of Apparel and Textiles requires only physical capital and labor, while the manufacture of Machinery requires capital, labor and human capital (H). Note as well that approaching a corner of the endowment simplex along a ray emanating from that corner represents an increase in the use (for an industry input vector) or abundance (for an endowment vector) of that factor, holding the concentration of other factors constant. Thus, Textiles use…

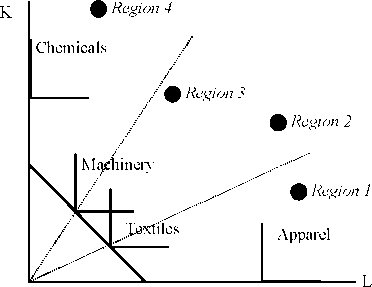
2.1. What if There Are More Sectors than Factors? Specialization of output across regions may not be indicative of a multiple cone equilibrium if prices are such that the number of sectors a region can produce profitably exceeds the number of factor inputs. This case is illustrated in figure 3, which exhibits a single cone of diversification anchored by four rather than two sectors. Because prices render the choice of product mix arbitrary, regions 2…

2. Single versus Multiple Cone Heckscher-Ohlin Equilibria The easiest way to build intuition for single versus multiple cone equilibria is to assume there are just two factors of production and that the world is even in the sense that regions produce just two goods at every stage of their economic development. Such a world is captured by the Lerner (1952) diagram displayed in figure 1. This figure contains unit value isoquants for four sectors, Apparel,…