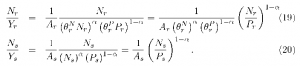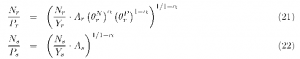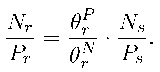Solving for the input-output ratios in terms of the ratio of observed factor inputs in the two regions, we get
Rearranging terms, we can write the observed factor inputs in terms of the observed unit factor requirements,
Under the maintained hypothesis of RFPEQ, we can solve for the relationship between the observed factor ratios by equating the relative wages paid to the true labor inputs across the regions, yielding
In words, the observed, unadjusted, input ratios will differ by exactly their relative quality adjustments.
Suppose RFPEQ does not hold and let the true quality adjusted relative factor returns vary across regions by a multiplicative factor, Yr. When Yr = 1, then relative factor price equality fails to hold between the two regions, i.e.
In terms of observed factors ratios, we now have
and substituting equations 21 and 22 into equation 24, we can express the unit factor requirement in region r in terms of the unit factor requirement in region s,
Equation 25 reveals several problems with any empirical implementation using unit input requirements to test for RFPEQ. Most importantly, there is a problem with identification in that specification 25 cannot separately identify the differences in regional Hicks-neutral productivity, Ai, differences in factor quality across regions,, and differences in factor prices across regions, 7r, all of which only vary across regions. Furthermore, adding additional factors to the production function does not solve the problem but merely adds more factor-specific productivity shifters to be estimated.
4.2. Testing one cone versus many (RFPEQ)
We now outline our preferred techniques for testing the competing hypotheses of one versus many cones. We start by considering the predictions from the RFPEQ theorem and then the FPEQ theorem. Finally we develop a technique for grouping regions into cones in the event that the single cone hypothesis has been rejected.
Under the null of RFPEQ across all regions, every region should have the same wagebill ratio within an industry and this should be equal to the average for the US,
The simplest test is a regression of the form:
where WBRfJs is the average relative wagebill for industry i in the US for a pair of factors f and g, and afg’s are coefficients on a vector of region dummies. Under the null hypothesis of RFPEQ, afg = 0 for all regions and factor pairs. Note that in order to estimate equation 26 for any factor pair including capital, one would have to construct a measure of capital payments as they are not usually recorded directly in the data. One possible solution is construct capital payments as the residual of value-added after payments to the two types of labor,
capital payments^ = Yjr — wagebilljNr — wagebilljpr.
However, this measure is particularly noisy in the plant data that we employ. We therefore focus our empirical work on relative wages.