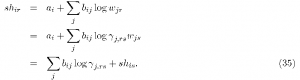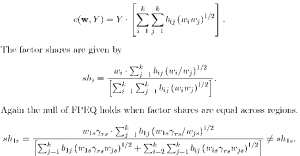A FPEQ and generalized cost functions
In this appendix, we consider tests of FPEQ for alternate cost functions using the factor share methodology developed for the CES production function.
A1. The translog cost function
The translog cost function with constant returns to scale is given by
Subject to the usual restrictions to ensure homogeneity in prices, the factor shares, sj = wjxj/c(wj, Y), are linear in the parameters and are given by
Under the null of FPEQ, factor shares will be equal in different regions so long as the cost functions are identical, i.e. identical technologies.
However, the failure of FPEQ will lead to variations in factor shares across regions. For example, if Wjr = 7j rsWjs across regions r and s, then the relationship between the factor shares in the two regions are given by
Note that, as in the CES case, using factor shares to test for FPEQ avoids any problems with unobserved differences in factor quality, the factor prices are for quality adjusted factors. Unlike the CES case, the difference in factor shares is linear in the factor price differences, not multiplicative. In addition, there is no way to back out the relative factor prices if more than one factor price varies across regions. However, the basic test remains the same in that the failure of factor shares to be the same within an industry is sufficient to reject FPEQ.
A2. The Diewert cost function
The Diewert cost function with constant returns to scale is given by
Again, while significant differences in iactor shares are sufficient to reject FPEQ, obtaining estimates of the y’s is not possible without imposing additional structure on the cost function.