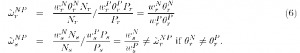Under RFPEQ, the observed relative wages will only equal the true relative wages if the quality adjustments are the same for the two labor types across regions.
For observed demands of the two labor types by the industry in the two regions, under the maintained assumption of RFPEQ we can solve for the relationship between the factor ratios in the two regions,
The observed, unadjusted, input ratios will differ by exactly their relative quality adjustments.
Now we consider the possibility that RFPEQ does not hold and let the true quality adjusted relative factor returns vary across the two regions by a multiplicative factor, y.8 For our three factor world, we need two y’s, YNP and yKP. The third factor price adjustment is given by
When any y = 1, then relative factor price equality fails to hold between the two regions, i.e.
In terms of observed factors, we now have
with similar relationships for the other factor ratios.
This equation demonstrates the crux of the problem with using observed factor inputs to test for RFPEQ. Unless the regional quality adjustment is assumed to be identical for all factors, then relative input intensities cannot reveal whether 7 =1.
In terms of observed relative wages from equation 6, we find
A close examination of equations 10 and 11 is useful for building intuition. Suppose RFPEQ holds (i.e. 7 =1) and that region r non-production workers are of higher relative quality (i.e. 0^ > ). Then equation 11 implies that the observed non-production to production wage ratio is higher in region r than region s.