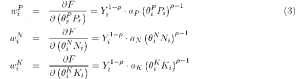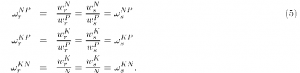While we will make use of the theorems in looking for deviations from factor price equality (FPEQ) and relative factor price equality (RFPEQ) across regions within the US, the theory and empirical methodology can be applied to any tests of factor price equality.
To develop our empirical framework, we impose some additional structure in the form of restrictions on the class of production functions. We restrict our analysis to the class of CES production technologies.7 For the purposes of exposition, we consider an economy with two regions (r and s) and one homogenous industry with three inputs and a CES value-added production function. We allow for the possibility that there are unobserved productivity differences between region r and region s which affect all factors equally. In addition, we allow for unobserved differences in factor quality between the two regions. Throughout the section, subscripts refer to regions and superscripts refer to factors. We start with a value-added production function common to the industry in both regions,
where Pi, N and Ki are observed production worker, non-production worker and capital inputs and Pi, Ni, and Ki are the true quality adjusted inputs in each region. Ai is a region-specific, Hicks-neutral productivity shifter. The actual production functions are CES in quality-adjusted inputs
where 1/1 — p is the elasticity of substitution between factors.
Given price-taking in the factor market and common output prices, the first order conditions for quality adjusted factors in each region are:
These three conditions give the returns for quality-adjusted factors. We maintain the assumption that factors are paid their true marginal product, i.e. they are compensated for quality. Since we are interested in the possibility of detecting deviations from factor price equality, we must pay particular attention to the difference between quantities (and prices) for observed and quality-adjusted factors.
For the purpose of exposition assume there are two regions, r and s, where region s is the reference region whose factors are taken to be the baseline quality benchmarks without loss of generality, i.e. = 1. The two regions are in a single cone of factor price equality, FPEQ, if
all hold simultaneously. In words, this means that the quality adjusted returns are identical for all factors. RFPEQ holds if any two of the following three conditions hold:
Note that the conditions for both FPEQ and RFPEQ are for quality-adjusted factor prices which cannot be observed in practice. In the following sections we develop empirical implications of RFPEQ and FPEQ for variables we can observe.