FACTOR PRICE EQUALITY AND THE ECONOMIES OF THE UNITED STATES: Substitutable

2.1. What if There Are More Sectors than Factors?
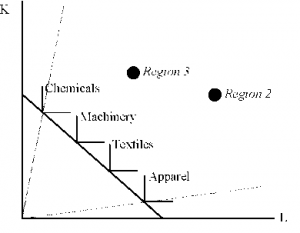
Specialization of output across regions may not be indicative of a multiple cone equilibrium if prices are such that the number of sectors a region can produce profitably exceeds the number of factor inputs. This case is illustrated in figure 3, which exhibits a single cone of diversification anchored by four rather than two sectors. Because prices render the choice of product mix arbitrary, regions 2 and 3 may not produce the same mix of sectors even though they inhabit the same cone. Region 3, for example, might produce Chemicals and Textiles and region 2 might produce Machinery and Apparel. Unevenness also implies that regions in neighboring cones may no longer produce at least one good in common. On the other hand, there remains a link, albeit weaker, between the probability that a region produces a sector and the similarity of the region’s factor endowments with the industry’s input intensity.
2.2. What if Factor Inputs are Substitutable?
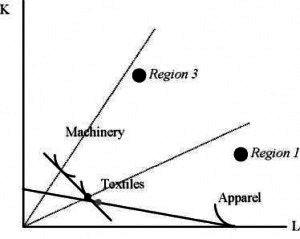
If production technologies allow for the substitutability of inputs, it is no longer true that regions from neighboring cones must produce common goods with identical techniques. In figure 4, for example, regions 1 and 3 both produce Textiles, but region 3 produces the sector with a more capital intensive technique. In this case, regions in the same cone use identical techniques, while regions in disparate cones use techniques that are closer to their endowments.
2.3. What if There are More Than Two Factors?
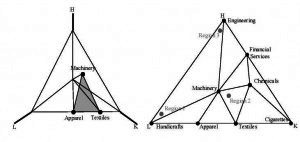
The key complication of considering higher dimensional factor spaces is that with F factors, regions can produce up to F — 1 goods in common, and therefore identifying a particular cone’s neighbors can be quite complex. The first panel of figure 5 illustrates the mechanics of generalizing a two factor HO model to three dimensions. The trick, noted by McKenzie (1955) and Leamer (1987) is to construct an endowment simplex by reducing a three dimensional factor space of capital (K), labor (L) and human capital (H) to a two dimensional simplex. This simplex is formed by intersecting the positive orthant of the factor space with a plane so that the coordinate axes of the factor space are represented by the corners of the endowment simplex, while the industry-input and country-endowment vectors are represented by points on the surface of this triangle. Thus, cones of diversification are represented by triangles on the surface of the simplex. In the figure, the shaded triangle represents a cone anchored by Machinery, Textiles and Apparel. The tilt of this triangle is determined by the three product prices and is analogous to the slope of the isocost line in the earlier Lerner diagrams.

Figure 3: Unevenness

Figure 4: Substitutability

Figure 5: Heckscher-Ohlin Specialization with Many Factors and Goods