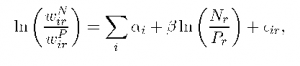FACTOR PRICE EQUALITY AND THE ECONOMIES OF THE UNITED STATES: Relaxing The Basic Assumptions

If we relax the standard assumptions of the Heckscher-Ohlin model it becomes much more difficult to distinguish empirically a multiple from a single cone equilibrium. Indeed, as indicated in figure 6, we are left with three types of tests:
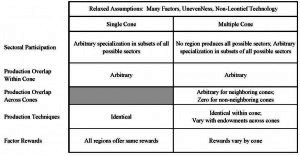
1. PRODUCT MIX: If all regions produce the same group of sectors, the US is characterized by a single cone equilibrium.4 This implication is easy to verify but not very satisfying because the absence of production overlap does not imply existence of multiple cones. Figure 7, for example, reports that US regions do not in fact all produce the same mix of goods, though the extent of overlap is increasing with time. The first panel of the figure indicates that the median percent of regional participation across within a four digit Standard
Industrial Classification sector rose from 28% in 1972 to 37% in 1992. Interestingly, there are some sectors that all regions produce, though it is possible that these sectors are non-tradeables. The second panel of the figure reports that most regions produce relatively few industries, that there are no regions that produce all industries, and that regional coverage also is increasing with time. Finally, the third panel reveals that the bilateral overlap of industries across region-pairs has also edged up with time.5 Nevertheless, all we can conclude from this evidence is that the existence of a multiple cone equilibrium cannot be ruled out.
2. PRODUCTION TECHNIQUE: If production techniques for commonly produced goods are identical, the US is characterized by a single cone equilibrium. On the other hand, evidence that production techniques vary with regional endowments is evidence for the multiple cone model. For any pair of regions one can test whether industries produced in common have techniques that vary systematically with the differences in relative endowments.
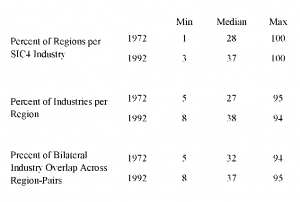
3. RELATIVE WAGES: If relative wages vary with regional endowments in the manner suggested above, the US cannot be characterized by a single cone equilibrium. We can test this implication by regressing log relative raw wages on log relative raw endowments, or

where w, N, P, i and r represent wages, non-production (skilled) workers, production (unskilled) workers, industry and region, respectively. Results of this regression are reported in figure 8. They indicate that regions relatively abundant in skilled workers receive relatively lower wages in both 1972 and 1992. This result is suggestive of the failure of relative factor price equality. In the next section, we develop a stronger test that is robust to potential unobserved heterogeneity of factors across regions.

Figure 6: Testing Factor Price Equality — Relaxed Assumptions

Figure 7: Industry Overlap Across US Regions

Figure 8: Regressing Regional Relative Wages on Regional Endowments