Introduction Among the central issues in macroeconomics is the nature of short run inflation dynamics. This matter is also one of the most fiercely debated, with few definitive answers available after decades of investigation. At stake, among other things, is the nature of business cycles and what should be the appropriate conduct of monetary policy. In response to this challenge, important advances have emerged recently in the theoretical modeling of inflation dynamics. This new literature…
Our results suggest that, conditional on the path of real marginal costs, the baseline new Phillips curve with forward looking behavior may provide a reasonably good description of inflation dynamics. When tested explicitly against an alternative that allows for a fraction of price setters to be backward looking, the structural estimates suggest that this fraction, while statistically significant, is not quantitatively important. One qualification, however, is that there is some imprecision in our estimates of…
We first describe our econometric specification of the new Phillips curve, along with our general estimation procedure. We then present both reduced form and structural estimates of the model. 3.1 Econometric Specification We begin by describing how we obtain a measure of real marginal cost. For simplicity, we restrict ourselves to the simplest measure of marginal cost available, one based on the assumption of a Cobb-Douglas technology. Let At denote technology, Kt capital, and Nt…
General Information As mentioned, Leon Tamaris & Co is a Greek company producing women’s footwear since 2000. In the beginning the company was only importing shoes and was the Greek representative of German firms. The company is based in Athens and has representatives in the rest of Greece. The company had its premises at the industrial district of Taurus near the center of Athens. It had an office and a small production unit. In 2005,…

The final version of the design for the IMF and the World Bank was an amalgam of proposals by White and Keynes, with a preponderance of White’s proposals. He prepared and represented U.S. views on the shape of the postwar international financial order. The competing plan by Keynes represented British views.
White’s unpublished papers of 1936-46 (in the Seeley G. Mudd Manuscript Library, Princeton University) include memoranda on the advantages stabilization funds provide, and on the desirability of providing stabilization loans to Mexico, China, and Brazil; drafts ofletters for Secretary Morgenthau to send to Roosevelt on international policy; a report on Cuba’s monetary and credit problems. As is clear from our earlier comments, White also was engaged, at Morgenthau’s direction, in drafting the proposal for establishing the IMF.
As an employee of the Treasury Department, White was well-informed about three of its initiatives in the operation of the ESF. One was the formulation of the elements of stabilization agreements with selected countries. The second was the conduct of the Tripartite Agreement. The third was ESF dealings in markets for foreign exchange, gold, silver, and government securities. We discuss the part each played in the formation ofWhite’s conception of the IMF. We then explore three sources ofWhite’s ideas about the principles to guide the organization of a bank for development loans: the ESF, a memorandum on a proposal for Latin American loans, and the stillborn Inter-American Bank.
2.1 ESF Stabilization Loans
The first stabilization loan that the ESF extended was to Mexico in January 1936. We do not know who in the Division ofResearch and Statistics at the Treasury devised the terms of the loan. White’s unpublished papers give no indication that he was a principal in the design of the loan, but he unquestionably was aware of its unique features. In any event, it became the model for subsequent stabilization loans to other countries in addition to Mexico. When he became the director of the division of monetary research in 1938, White administered stabilization loans.
The terms of the Mexican loan were enclosed in a letter to the Federal Reserve Bank of New York as the Treasury’s fiscal agent, which was instructed to send them to the Banco de Mexico. The letter follows:
“The Secretary of the Treasury of the United States has, as a result ofhis recent conversations in Washington with the Secretary of the Mexican Treasury, authorized us, as fiscal agent of the United States, to enter into the following arrangement with you, on behalf of the Republic of Mexico, for the purpose of supplying the Republic ofMexico with dollar exchange, from time to time, as may be required:
1. We, as fiscal agent of the United States, will purchase from you, from time to time, as requested by you, Mexican pesos, the pesos so purchased to be credited to us (as fiscal agent of the United States) on your books in a special account to be opened in the name of the “Federal Reserve Bank ofNew York as Fiscal Agent of the United States.” Interest at the rate of 3% per annum in to be credited on such account.
Upon receipt by us of advice by telegram that this account has been credited with a stated amount in Mexican pesos, we shall in turn credit you on our books in a special account to be opened in the name of“Banco de Mexico as Fiscal Agent of the Republic ofMexico” in an amount inU.S. dollars equal, at the then prevailing rate of exchange in New York for telegraphic transfers on Mexico, to the amount in pesos so credited to us on your books.
2. The total amount of pesos purchased by us from you and standing to our credit on your books as aforesaid, exclusive of interest, shall not at any time exceed in the aggregate the equivalent ofU.S. $5,000,000, computed at the actual buying rate for such pesos.
3. You agree that any or all pesos purchased by us from you, together with interest thereon as 
4. As security for the performance by you of your agreement to repurchase such pesos as aforesaid, you authorize and request Federal Reserve Bank ofNew York and Federal Reserve Bank of San Francisco to set aside from time to time and to pledge to Federal Reserve Bank ofNew York as fiscal agent of the United States, so much of the silver now held for your account under earmark by Federal Reserve Bank ofNew York and Federal Reserve Bank of San Francisco (amounting to approximately 11,000,000 ounces) as the dollar equivalent of pesos purchased and then standing to our credit on your books as aforesaid bears to U.S. $5,000,000; and in the event of your failure to repurchase such pesos as hereinabove provided, you do further authorize us as pledge aforesaid, to sell so much of such silver so held under pledge, at any time, at the so-called official price for silver as then quoted by Messrs. Handy & Harman, New York, New York, and to apply the proceeds thereof in such manner, as may be necessary to save us, as fiscal agent of the United States, and the United States, harmless from any loss by reason of any failure to repurchase said pesos as herein provided; and you do hereby authorize and request Federal Reserve Bank of San Francisco to honor any request made by us to hold or deliver for our account as fiscal agent of the United States, and as pledge aforesaid, any or all of the silver now held for your account under earmark by said Federal Reserve Bank of San Francisco.
5. Itis understood and agreed that our obligation, as fiscal agent of the United States, to purchase any amount of pesos pursuant hereto shall be conditional and dependent upon your maintaining with us and/or the Federal Reserve Bank of San Francisco, an amount of silver sufficient to secure, as hereinabove in paragraph 4 provided, your obligation to repurchase such pesos.
6. Itis understood you will take such further action as may be reasonably requested by us to effectuate the purposes and intent of this arrangement.
7. This arrangement shall continue in effect until February 1, 1936, and from month to month thereafter except that we, as fiscal agent of the United States, may on or before the fifteenth day of any month advise you that our offer to purchase pesos under this agreement, in so far as it has not been accepted, is to be discontinued at the end of that month.”
We comment on the unique features of this agreement. For the first time, so far as we are aware, instead of a loan of dollars by one country to another, the transaction is described as an exchange of currencies of the two contracting parties. The U.S. advanced $5 million to Mexico for pesos, which the Banco de Mexico agreed to repurchase on demand by the U.S. Treasury at any time at the exchange rate at which they had been acquired. Mexico, moreover, agreed to pay a 3% interest rate (the discount rate was then 1^%at the Federal Reserve Bank ofNew York, and the prevailing rate on 4- to 6- months commercial paper was 0.75%) on the peso account credited to the Bank. In addition, Mexico was required to provide silver collateral equal to the dollar amount of the exchange of currencies.
Collateral requirements were not uncommon during the interwar years. League ofNation loans were 
In section 3, we check the Articles of Agreement of the IMF to determine the extent of the influence of the ESF model stabilization agreement on the design ofIMF financial assistance to member countries.
2.2 ESFParticipation in the TripartiteAgreement
Before arriving at an agreement with the French and with the British in September 1936, the U.S. Treasury and members of Congress had regarded the British as an adversary in the foreign exchange market. Under the terms of the Agreement, which accepted a need for devaluation of the franc, the three countries plus Belgium, Switzerland, and the Netherlands, whichjoined later and also subscribed to it, adopted the principles of mutual consultation with respect to the level of exchange rates and reciprocity in gold dealings.
Each central bank committed to convert into gold the balance in its own currency that the other central bank had accumulated each day as a result of its exchange control operations and to make available from earmark gold to meet obligations undertaken by the foreign central bank as a result of such operations. In addition, the central banks agreed to advise each other daily of transactions as a result of which gold was earmarked or released.
One feature of the Tripartite Agreement thus was that it provided not for loans between the signatories but for an exchange of gold for currencies. A second feature was that, at least for each twenty-four hour period, debtors would not need to adjust exchange rates or apply exchange controls. The Agreement facilitated settlement of multilateral balances. A third feature was that, by mutual agreement between two countries, on twenty-four hours’ notice, a change in the exchange rate could be effected.
Cooperation and reciprocity among countries that the Tripartite Agreement fostered became principles that served as the bedrock of the IMF Articles of Agreement.
2.3 ESFDealings in the MarketsforForeign
Exchange, Gold, Silver, and GovernmentSecurities Intervention by the ESF in the exchange market was conducted on its behalfby the Federal Reserve Bank ofNew York, which was authorized to purchase or sell the kinds of exchange that the Treasury designated. The Treasury agreed to provide the dollars and foreign exchange required to fulfill the contracts the Bank entered into. The ESF’s intervention in support of the dollar involved sales of sterling and francs in New York or dollars bought in London and Paris for its account. Intervention in support of sterling or the franc involved purchases of sterling and francs bought in New York or dollars sold in London and Paris for its account, or by the purchase of sterling to pay for gold and silver bought in London. The way foreign central banks obtained a supply of dollars with which to intervene was that the Treasury earmarked gold abroad against an advance of dollars in New York or it purchased gold abroad against immediate payment in dollars.
The system ofU.S. gold regulations established under the Gold Reserve Act drew a distinction between foreign central banks that bought and sold gold at a fixed price and those that did not. No special license was required by central banks of gold standard countries to acquire gold from the U.S. Treasury as long as their exchanges were below gold export points.

The Tripartite Agreement led to a withdrawal of the forgoing gold regulations. A central bank of a country that adhered to the Agreement could not on its own account acquire gold from the U.S. Treasury and have it earmarked free for export at the Federal Reserve Bank ofNew York without a special license for each transaction, and even when acting as fiscal agent for its exchange stabilization fund or its government, it could not acquire gold from the U.S. Treasury and have it earmarked, unless twenty-four hours’ notice of the transaction had been given and special accounts had been set up for implementing the transaction.
The ESF was authorized to buy spot or forward silver in any market through the Federal Reserve Bank or its agents and to hold silver so bought in any one of fourteen foreign depositories located in London and New York. The ESF was also authorized to sell silver through the Federal Reserve Bank. The Fund sold gold for sterling, then bought silver abroad with sterling for sale to the Treasurer of the U.S. under the Silver Purchase Act of June 1934.
The ESF also bought silver elsewhere mainly from the Central Bank of China and the Banco de Mexico for dollars.
The ESF’s authority to invest in direct obligations of the U.S. in effect sanctioned it to engage in open market operations, but Morgenthau declared the primary purpose of the ESF in holding government securities was to obtain earning assets.
White’sjob afforded him the opportunity to familiarize himself with these activities of the ESF. In the section that follows we note the extent to which his experience influenced his vision of the ways in which the IMF might operate. Since the ESF was a domestic institution with international scope while the IMF was to be an intergovernmental institution that would have an international membership, the new institution could not be merely a carbon copy of the existing one. There was room for differences as well as similarities between the two.
2.4 Influences on White’s Design of the IBRD
White’s experience as a Treasury official made a contribution to several features ofhis plans for the IBRD. We note three events that were part ofhis experience and two features of the plan. The events are: (1) the Mexican stabilization loan of January 1936; (2) the undated (1939?) 6-page memorandum “Loans to Latin America for the Industrial Development ofLatin America”; (3) the proposals for an Inter-American Bank that originated in a meeting in Panama in 1939. The features of the IBRD are: (1) low-interest loans; (2) government guarantees of private investor loans. We comment on each event and feature.
1. The Mexican stabilization ESF loan that became the prototype for its pre-war lending was notable 
2. White’s memorandum included a proposal that the U.S. establish a bank with a capital of $300 million (funded by the ESF’s unused gold), authorized to issue up to $1.7 billion inU.S. government-guaranteed bonds, to make long-run loans for industrial enterprises in Latin America under the control of the borrowing country or its nationals. Loans would be offered at no more than 1 percent in excess of the cost ofborrowing by the bank. Three-quarters of the dollar loans was to be expended on imports from the U.S.
3. White was appointed by Morgenthau to serve on an interdepartmental committee on plans for an Inter-American Bank, the aim of which was to frustrate Nazi penetration in Latin America. The charter that was drafted in 1940 would have authorized the bank to make loans, or guarantee loans made by others, in any currency or gold to member governments, their nationals, fiscal agencies, and central banks.
Governments were to guarantee that loans of more than two-years maturity would be repaid. The Bank could hold obligations and securities of member governments, their currencies or foreign exchange, for its own account or the account of member governments. It could hold deposits of member governments, rediscount bills arising from intra-hemisphere trade that commercial banks discounted, and issue its own obligations. Only Mexico ratified the Inter-American Bank Convention. A U.S. Senate subcommittee, which held hearings on the subject in 1941, took no action. White, who championed economic assistance to Latin America, China, and the Soviet Union, extracted some of the elements in the Inter-American Bank proposal in preparing his blueprint for a World Bank.
4. One feature of the World Bank that White espoused was that it should make loans at artificially low (i.e., below market) interest rates (Oliver 1975, pp. 120-122). He insisted that the Bank should limit its loans to cases where otherwise private capital markets would lend at high (relative to those that would obtain in advanced countries) interest rates. In part, his attitude derived from his genuine concern to help the impoverished and war-torn countries of the rest of the world. White, however, in effect substituted the decision of the Executive Directors of the Bank for the market’s decision on which projects were worth funding to the extent that the lending decisions did not involve projects where the social return exceeded the private return and the private sector would not have funded them. In fact, many of the Bank’s loans in the 1950s and 1960s to finance steel mills and the like were abysmal failures (Krueger 1998). Because demand at artificially low interest rates exceeded supply, the IBRD had to ration its available funds among borrowers. It was decided in negotiations between the British and the Americans before Bretton Woods that the Bank would not differentiate among borrowers by varying the interest rate that it charged. If there was a difference in rates charged, it reflected the interest rate the Bank had to pay to obtain funds.
5. A second feature of the blueprint of the World Bank was the emphasis on the need for government guarantees of the repayment of private loans for reconstruction and long-run development. White was responding to the default on international loans in the 1930s and the concurrent shutoff of foreign lending. In order to generate a flow of private capital to foster capital formation and growth in the postwar period, White was convinced that government guarantees of the debts of private borrowers were essential.
In the next section, we compare the ESF and the IMF, noting the respects in which they were similar or differed. Low interest rates was not an ESF characteristic, but White introduced it into the IMF and the IBRD. Loan guarantees were not a characteristic of the ESF nor of the IMF, but White introduced them into the IBRD, possibly a legacy of the Tripartite Agreement.
In this case, Keynes at Bretton Woods supported White’s emphasis on Bank guarantees of private overseas investment.
A FPEQ and generalized cost functions In this appendix, we consider tests of FPEQ for alternate cost functions using the factor share methodology developed for the CES production function. A1. The translog cost function The translog cost function with constant returns to scale is given by Subject to the usual restrictions to ensure homogeneity in prices, the factor shares, sj = wjxj/c(wj, Y), are linear in the parameters and are given by Under the null…
In this paper, we provide a general methodology to test for factor price equality across economies. Under the usual HO assumptions of common products, common product prices, and common technologies, we develop testable implications of the Factor Price Equality Theorem and the Relative Factor Price Equality Theorem for a broad class of production technologies. Unlike previous attempts to formulate tests for FPEQ and RFPEQ, our testing methodology is robust to sources of unobserved heterogeneity that…
As described above, an additional implication of multiple factor price cones is that regions in non-neighboring cones are expected to have distinct mixes of goods. By determining the relationship between product mix overlap and cone assignments for pairs of regions, we can provide a robustness check on our results. More specifically, we estimate the number of industries two regions have in common as a function of their cone assignments where Irs is the number of…
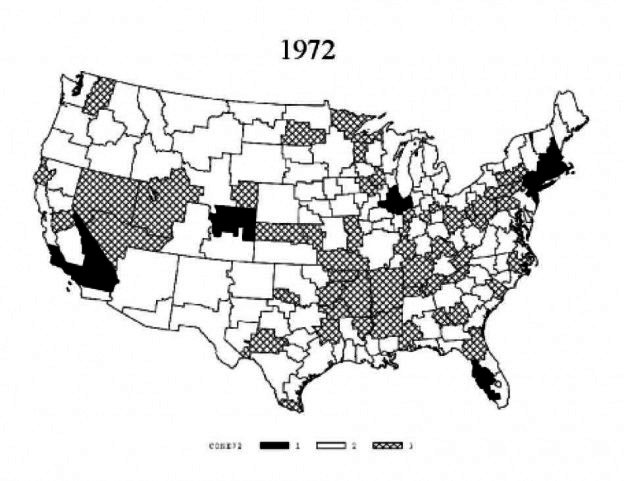
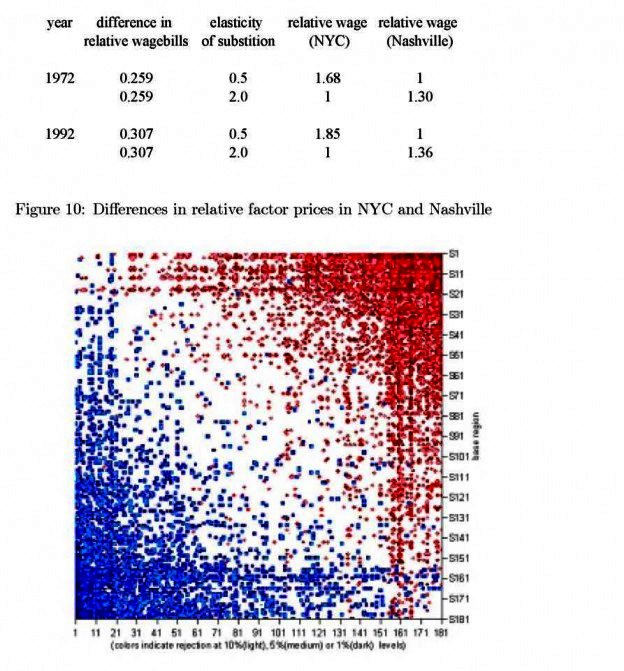
From Figure 9, we know that the single cone hypothesis can be easily rejected. Using those results and the methodology described above, we can produce factor price cones within the US based on relative wages for 1972 and 1992. Regions with significantly higher wagebill ratios are grouped in cone 1. For 1972, there are eight regions in this upper cone including large, urban labor markets such as New York City, Chicago, and Los Angeles. Regions…
We can now answer the question posed at the outset. Nashville and New York have significantly different relative wagebills for non-production and production workers, and thus significantly different relative wages. In fact, in 1972 the relative wagebill in Nashville is 11 percent below the US average while that for New York is 15% above. To map the estimated coefficients into differences in relative factor prices, we need to make assumptions about the elasticity of substitution….