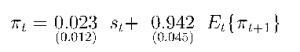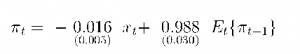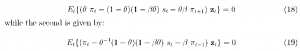INFLATION DYNAMICS AND LOAN SERVICE IN THE INTERNET: The New Phillips Curve: New Estimates of the New Phillips Curve

We first describe our econometric specification of the new Phillips curve, along with our general estimation procedure. We then present both reduced form and structural estimates of the model.

3.1 Econometric Specification

We begin by describing how we obtain a measure of real marginal cost. For simplicity, we restrict ourselves to the simplest measure of marginal cost available, one based on the assumption of a Cobb-Douglas technology. Let A_t denote technology, K_t capital, and N_t labor. Then output Y_t is given by

Real marginal cost is then given by the ratio of the wage rate to the marginal product of labor, i.e., Hence, given equation (12) we have:

where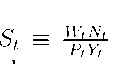 is the labor income share (equivalently, real unit labor costs)..

Letting lower case letters denote percent deviations from the steady state we have:

where z_t is a vector of variables dated t and earlier (and, thus, orthogonal to the inflation surprise in period t + 1). The orthogonality condition given by equation (17) then forms the basis for estimating the model via Generalized Method of Moments (GMM).

The data we use is quarterly for U.S. over the period 1960:1 to 1997:4. We use the (log) labor income share in the non-farm business sector for s_t. Our inflation measure is the percent change in the GDP deflator. We use the overall deflator rather than the non-farm deflator for most of our analysis because we are interested evaluating how well our model accounts for the movement in a standard broad measure of inflation. We show, however, that our results are robust to using the non-farm deflator. Finally, our instrument set includes four lags of inflation, the labor income share, output gap, the long-short interest rate spread, wage inflation, and commodity price inflation.

Combining equations (14) and (3) yields the inflation equation:

Since under rational expectations the error in the forecast of n_t+1 is uncorrelated with information dated t and earlier, it follows from equation (14) that

3.2 Reduced Form Evidence

We first report our estimate of equation (17). We refer to this evidence as “reduced form” since it contains an estimate of the overall slope coefficient on marginal cost, A, but not of the structural parameter 6 (the measure of price rigidity) that underlies A (see equation 16). The resulting estimated equation is given by λ

Overall, the estimated new Phillips curve is quite sensible. The slope coefficient A on real marginal cost is positive and significant, as is consistent with the a priori theory. The estimate of the coefficient on expected inflation, the subjective discount factor ft, is also reasonable, particularly after accounting for the sampling error implied by the estimated standard deviation.15 Thus, at first pass, it appears that the new Phillips curve provides a reasonable description of inflation. If you do not want to live under constrained conditions, you may check out the web site speedy-payday-loans.com to more about their offeres. The idea is to carry out such a business in the Internet attracts much attention without any hesitation.

To highlight the virtues of using real marginal cost as the relevant real sector driving variable in the new Phillips curve, we reestimate equation (6), using detrended log GDP as a proxy for the output gap xt:

The model clearly doesn’t work in this case: the coefficient associated with the output gap is negative and significant, which is at odds with the prediction of the theory. This finding, of course, is completely consistent with our earlier result that, when the model is reversed and estimated in the form of the old Phillips curve, the coefficient on the lagged output gap is positive (see equation (9)). Thus, it is the use of real marginal cost over the output gap, and not the estimation strategy, that accounts for the econometric success of the new Phillips curve.

3.3 Structural Estimates

We now redo the exercise in a way that allows us to obtain direct estimates of the structural parameter 0. In particular, we substitute the relation for A, equation (16), into equation (17) to obtain an econometric specification that is nonlinear in the structural parameters 0 and ft.

One econometric issue we must confront is that, in small samples, nonlinear estimation using GMM is sometimes sensitive to the way the orthogonality conditions are normalized. For this reason, we use two alternative specifications of the orthogonality conditions as the basis for our GMM estimation procedure. The first specification takes the form

We estimate the structural parameters 0 and ft using a nonlinear instrumental variables estimator, with the set of instruments the same as is in the previous case. For robustness, we consider two alternatives to the benchmark case. In the first alternative we restrict the estimate of the discount factor ft to unity. In the second, we use the non-farm GDP deflator as opposed to the overall deflator. Finally, we estimate each specification using the two different normalizations, as given by equations (18) and (19).

The results are reported in Table 1. The first two columns give the estimates of 0 and ft. The third then gives the implied estimate of A, the reduced form slope coefficient on real marginal cost. In general, the structural estimates tell the same overall story as the reduce form estimates. The implied estimate of A is always positive and is highly significant in every case but one (restricted /3, normalization (2)). The estimate of /3 in the unrestricted case is somewhat low, but not unreasonably so, given the sampling uncertainty. Are you tired thinking about money lack? To solve this problem you may take a speedy loan to live till wage is received.

The estimate of the structural parameter 6 is somewhat large and also somewhat sensitive to the normalization in the GMM estimation. Using method (1), we estimate 6 to be around 0.83 with a small standard error, which implies that prices are fixed for between roughly five and six quarters on average. That period length is close to the average price duration found in survey evidence, though perhaps on the high side. Method (2) yields a slightly higher estimate of 6, around 0.88. Since A is decreasing in 6 (greater price rigidity implies that inflation is less sensitive to movements in real marginal cost), the higher estimates of 6 implies a lower estimate of A for method (2).

For several reasons, however, our estimates of the degree of price rigidity are likely to be upward biased. First, it is likely that the labor share does not provide an exact measure of real marginal cost. In this instance, the estimate of the slope coefficient A is likely to be biased towards zero. This translates into upward bias of 6, given the inverse link between the two parameters. Second, the underlying theory that is used to identify 6 from estimates of A, assumes a constant markup of price over marginal cost in the absence of prices rigidities. If the markup in the frictionless benchmark model were countercyclical, as much recent theory has argued, the implied estimate of 6 would be lower.18 With a countercyclical markup, desired price setting is less sensitive to movements in marginal cost, which could help account for low overall sensitivity of inflation to the labor share.

The model also works well in the sense that we do not reject the overidentifying restrictions. Though we do not report the results here, the p-values for the null hypothesis that the error term is uncorrelated with the instruments are all in the range of 0.9 or higher. This kind of test has low power, however, since it is not applied against any specific alternative hypothesis. In the next section we develop a more refined test to measure how well the model accounts for inflation dynamics.

Table 1: Estimates of the New Phillips Curve