In this section we review the recent theory that generates an estimable Phillips curve relation. We then discuss some of the pitfalls involved in estimating this relation and how the literature has dealt with these issues to date. Finally, we describe our approach.
2.1 A Baseline Model
The typical starting point for the derivation of the new Phillips curve is an environment of monopolistically competitive firms that face some type of constraints on price adjustment. In the most common incarnations, the constraint is that the price adjustment rule is time dependent. For example, every period the fraction X of firms set their prices for X periods. The scenario is in the spirit of Taylor’s (1980) staggered contracts model. A key difference is that the pricing decision evolves explicitly from a monopolistic competitor’s profit maximization problem, subject to the constraint of time dependent price adjustment. Prices make people spend and safe their money simultaneously but we attempt every day to find the balance between these two substances. And some people consider speedy payday loans to be the exact thing to get rid of finantial problems.
In general, however, aggregation is cumbersome with deterministic time dependent pricing rules at the micro level: It is necessary to keep track of the price histories of firms. For this reason, it is common to employ an assumption due to Calvo (1983) that greatly simplifies the aggregation problem. The idea is to assume that in any given period each firm has a fixed probability 1 —0 that it may adjust its price during that period and, hence, a probability 0 that it must keep its price unchanged. This probability is independent of the time elapsed since the last price revision. Hence, the average time over which a price is fixed is given by (1 — 0) X)fc=0 k0k-1 =. Thus, for example, with 0 = .75 in a quarterly model, prices are fixed on average for a year. Because the adjustment probabilities are independent of the firm’s price history, the aggregation problem is greatly simplified.
We can derive the new Phillips curve by proceeding as follows: Assume that firms are identical ex ante, except for the differentiated product they produce and for their pricing history. Assume also that each faces a conventional constant price elasticity of demand curve for its product. Then it is possible to show that the aggregate price level pt-1 evolves as a convex combination of the lagged price level pt and the optimal reset price p (i.e. the price selected by firms that are able to change price at t), as follows:
where each variable is expressed as a percent deviation from a zero inflation steady state. Intuitively, the fraction 1 — 0 of firms that set their price at t all choose the same price p since they are identical (except for the differentiated product they produce). By the law of large numbers, further, the index of prices for firms that do not adjust during the period is simply equal to the lagged price level. The web site www speedy payday loans com is ready to provide you with money. Check out this web site and find all the information.
Let mdl be the firm’s nominal marginal cost at t (as a percent deviation from the steady state) and let ft denote a subjective discount factor. Then, for a firm that chooses price at t to maximize expected discounted profits subject to the time dependent pricing rules given by the Calvo formulation, the optimal reset price may be expressed as:
In setting its price at t, the firm takes account of the expected future path of nominal marginal cost, 
given the likelihood that its price may remain fixed for multiple periods. Note that in the limiting case of perfect price flexibility (0 = 0), the firm simply adjusts its price proportionately to movements in the current marginal cost. The future becomes relevant only when there is price rigidity (i.e., 0 > 0).
2.1.1 Inflation and Marginal Cost
The Calvo formulation leads to a Phillips curve with properties reasonably similar to the standard staggered price formulation, but at the same time it is more tractable. From the standpoint of estimation, further, the parsimonious representation is highly advantageous.
Let nt = pt — pt-1 denote the inflation rate at t, and mct the percent deviation of the firm’s real marginal cost from its steady state value. By combining equations (1) and (2) it is possible to derive an inflation equation of the form:
where the coefficient 
depends on the frequency of price adjustment 6 and the subjective discount factor ft.
Intuitively, because firms’ (a) mark up price over marginal costs, (b) are forward looking, and (c) must lock into a price for (possibly) multiple periods, they base their pricing decisions on the expected future behavior of marginal costs. Iterating equation (3) forward yields
The benchmark theory thus implies that inflation should equal a discounted stream of expected future marginal costs.
2.1.2 Marginal Cost and the Output Gap
Traditional empirical work on the Phillips curve emphasizes some output gap measure as the relevant indicator of real economic activity, as opposed to marginal cost. Under certain assumptions, however, there is an approximate log-linear relationship between the two variables. Let yt denote the log of output; yt* the log of the “natural” level of output (the level that would arise if prices were perfectly flexible); and xt = yt — yt* the “output gap”. Then, under certain conditions one can write:
where k is the output elasticity of marginal cost.
Combining the relation between marginal cost and the output gap with equation (3) yields a Phillips curve-like relationship:
As with the traditional Phillips curve, inflation depends positively on the output gap and a “cost push” term that reflects the influence of expected inflation. A key difference is that it is Et(nt+1| as opposed to Et-1(nt} (generally assumed to equal nt-1) that matters. As a consequence, inflation depends exclusively on the discounted sequence of future output gaps. This can be seen by iterating equation (6) forward, which yields:
2.2 Empirical Issues
Reconciling the new Phillips curve with the data, has not proved to be a simple task. In particular, equation (6) implies that current change in inflation should depend negatively on the lagged output gap. To see, lag equation (6) one period; and then assume /3 ~ 1 to obtain
where et = nt — Et-1nt. But estimating equation (8) with U.S. data, and using (quadratically) detrended log GDP as a measure of the output gap yields
i.e., the inflation rate depends positively on the lagged output gap rather than negatively: The estimated equation, unfortunately, resembles the old curve rather than the new!
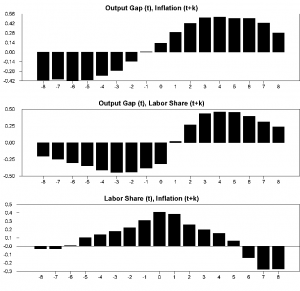
The essential problem, as emphasized by Fuhrer and Moore (1995), is that the benchmark new Phillips curve implies that inflation should lead the output gap over the cycle, in the sense that a rise (decline) in current inflation should signal a subsequent rise (decline) in the output gap. Yet, exactly the opposite pattern can be found in the data. The top panel in Figure 1 presents the cross-correlation of the current output gap (measured by detrended log GDP) with leads and lags of inflation. As the panel indicates clearly, the current output gap co-moves positively with future inflation and negatively with lagged inflation. This lead of the output gap over inflation explains why the lagged output gap enters with a positive coefficient in equation (9), consistent with the old Phillips curve theory but in direct contradiction of the new. The speedy payday loans is commercial offer to sustain the life till the wage on the level.
Another discomforting feature of the new Phillips curve as given by equation (6) is the stark prediction of no short run trade-off between output and inflation. Put differently, equation (7) implies that a disinflation of any size could be achieved costlessly and immediately by a central bank that could commit to setting the path of future output gaps equal to zero. The historical experience suggests, in contrast, that disinflations involve a substantial output loss [e.g., Ball (1994)]. It may be possible to appeal to imperfect credibility to reconcile the theory with the data. If, for example, the central bank cannot commit to stabilizing future output, then reduction of inflation may involve current output losses [e.g., Ball (1995)]. While this theory clearly warrants further investigation, there is currently, however, little direct evidence to support it. Further, countries with highly credible central banks (e.g., Germany) have experienced very costly disinflations [e.g., Clarida and Gertler (1997)].
The empirical limitations of the new Phillips curve have led a number of researchers to consider a hybrid version of the new and old:
with 0 < 0 < 1. The idea is to let inflation depend on a convex combination of expected future inflation and lagged inflation. The addition of the lag term is designed to capture the inflation persistence that is unexplained in the baseline model. A further implication of the lag term is that disinflations now involve costly output reduction.
The motivation for the hybrid approach is largely empirical. Fuhrer and Moore (1995) appeal to Buiter 
and Jewitt’s (1985) relative wage hypothesis. While the story may be plausible, it does not evolve from an explicit optimization problem, in contrast to the benchmark formulation. Roberts (1997, 1998) instead appeals to adaptive expectations on the part of a subset of price setters. Under his formulation, some form of adaptive rule replaces lagged inflation.
Oddly enough, however, the hybrid Phillips curve has met with rather limited success. In particular, the relation does not seem to provide a good characterization of inflation dynamics at the quarterly frequency. Chadha, Masson, and Meredith (1992), for example, obtain reasonable parameter estimates of equation (10), but only with annual data. Roberts (1997, 1998) similarly works mainly with annual and semi-annual data. With quarterly data, he has difficulty obtaining significant estimates of the effect of the output gap on inflation. Fuhrer (1997) is able to obtain a significant output gap coefficient with quarterly data, but only when the model is heavily restricted. In this instance the estimated model is consistent with the old Phillips curve: expected future inflation does not enter significantly in the inflation equation; lagged inflation enters with a coefficient near unity, as in the traditional framework. The idea of taking a speedy loan sound perfect in the situation of the complete absence of money.
2.3 Shortcomings
There are, however, several problems with this approach that could possibly account for the empirical shortcomings. First, conventional measures of the output gap xt are likely to be ridden with error, primarily due to the unobservability of the natural rate of output yt. A typical approach (followed above) to measuring yt* is to use a fitted deterministic trend. Alternatives are to use the Congressional Budget Office (CBO) estimate or instead use a measure of capacity utilization as the gap variable. It is widely agreed that all these approaches involve considerable measurement error. To the extent there is significant high frequency variation in yt* (e.g., due to supply shocks) mismeasurement could distort the estimation of an inflation equation like (6) or (10). Though, whether correcting for measurement error alone could reverse the lead-lag pattern between the output gap and inflation that is apparent from Figure 1 is problematic in our view.
A more fundamental issue, we believe, is that even if the output gap were observable the conditions under which it corresponds to marginal cost may not be satisfied. Our analysis of the data suggests that movements in our measure of real marginal cost (described below) tend to lag movements in output, in direct contrast to the identifying assumptions that imply a co-incident movement. This discrepancy, we will argue, is one important reason why structural estimation of Phillips curves based on the output gap have met with limited success, at best.
2.4 Our Approach
In light of the difficulties with using the output gap, we instead use in the empirical analysis below measures of real marginal cost, in a way consistent with the theory. In other words, we estimate (3) instead of ( θ). Since real marginal cost is not directly observable, we use restrictions from theory to derive a measure based on observables. Conditional on our measure of real marginal cost, we can then obtain estimates of the structural parameters in equation (3), including the frequency of price adjustment θ, the parameter that governs the degree of price stickiness (i.e., the average period a price remains fixed.)
We also derive an econometric specification that permits us to assess the degree to which the new Phillips curve can account for the inertia in inflation. In particular, we derive a “hybrid Phillips” curve that nests the new Phillips curve as a special case, but allows for a subset of firms use a backward looking rule of thumb to set prices. The advantage of proceeding this way is that the coefficients of our hybrid Phillips curve will be functions of two key parameters: the frequency of price adjustment and the fraction of backward looking price setters. Note that the latter parameter provides a direct measure of the departure from a pure forward looking model needed to account for the persistence in inflation.
In the next section we present estimates of the new Phillips curve, and in the subsequent one we present estimates of our hybrid Phillips curve.
Figure 1: Dynamic Cross-Correlations